一、题型特征
提问方式:至少……才能保证……
二、求解
最不利情况种数+1
三、例题
例1:现有红、黄、蓝、黑、白五种颜色的卡片各20张,都装在一个密封小纸盒里,随机从纸盒中抽取卡片,为保证抽出的卡片至少有两张颜色相同,则最少应抽出几张卡片?
A.5 B.6
C.7 D.8
【解析】B。
考虑最差情况,五种颜色的卡片各抽出一张,然后随意抽出一张即可满足条件,因此最少应抽出 5+1=6 张。选B。
例2:某研究所有三种学历的工作人员:博士3人、硕士6人、本科生8人。现在将每个人进行编号抽签,为了保证一次性选出6个相同学历的人员,则至少要抽取( )个签。
A.13 B.14
C.15 D.16
【解析】B。
考虑最差情况,抽出博士3人、硕士5人、本科生5人,只要再抽出1人即可满足条件,所求为 3+5+5+1=14个签,选 B。
例3:梅花小区组织党员参与“两学一做”相关主题演讲、征文、摄影、书法和绘画五项比赛,要求每名党员参加其中的两项,无论怎么安排都发现至少有 7 名党员参加的培训内容完全相同,问小区至少有( )名党员。
A.50 B.51
C.60 D.61
【解析】D。
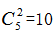
从五项比赛中选择两项共有种情况,故小区至少有10×6+1=61 名党员,选D。
所以大家在做最不利原则问题的时候,先学会判断题目是否属于最不利原则题目,如果是的话,就直接“最不利情况种数+1”即可。小编希望以上内容对大家解题有所帮助,大家也可以关注我们,我们会给大家提供更多有用的、容易掌握的解题小技巧。











