笔试中有一门科目为数量关系,其研究的是数与数之间的量化关系,考查的是奥数思维。数量关系的题型有很多种,工程、行程、经济利润、几何、排列组合等必考题型,其中一种较为简单的题型是工程问题,考查的一种形式是水池模型的变形,牛吃草模型。
(一)认识牛吃草模型
牛吃草模型之所以是工程问题,是因为其反映的是两个主体牛以及草,因为工作效率的不同,而产生的不同工作结果。也可以将牛吃草问题想象成行程问题,牛在以较快的速度吃草地上的草,草以较慢的速度在增长满足牛的消耗,本质上就是追及模型。
【示例】某奶牛公司拥有一片草地,该草地以均匀的速度生长,已知该草地可供200只奶牛吃30天,180只奶牛吃50天。如果该公司在该草地只饲养了160只奶牛,则可供这些奶牛吃多少天。
【分析】在这道题目中,草以一定的速度在增长,牛以一定的速度在吃草,牛越多,可供消耗的天数就越少,这就是牛吃草模型。
(二)牛吃草的基础考查形式
牧场上有一片匀速生长的草地,放N头牛去吃草且每头牛每天吃的草量相同。牛吃草使草量减少,草自身生长使草量增加,(前提:牛吃草的速度大于草自身生长的速度),这种情况称之为供不应求。假设T天牛把草吃完,同时假设这片草场原有量为y份,每头牛每天吃1份草,这片草场的草每天的生长速度为x份。则原有草量=(牛每天吃掉的量-草每天生长的量)×天数,整理可得:y=(N-x)×T。
【例1】某疫苗接种点市民正在有序排队等候接种。假设之后每小时新增前来接种疫苗的市民人数相同,且每个接种台的效率相同,经测算:若开8个接种台,6小时后不再有人排队;若开12个接种台,3小时后不再有人排队。如果每小时新增的市民人数比假设的多25%,那么为保证2小时后不再有人排队,需开接种台的数量至少为:
A. 14个 B. 15个
C.16个 D. 17个
【解析】根据牛吃草公式y=(N-x)T,y代表原有草量,即原有排队的市民数;N代表牛的头数,即所开接种台数量;x为草生长的速度,即每小时新增市民数;T代表时间。代入数据,y=(8-x)×6,y=(12-x)×3,解得x=4,y=24,每小时新增市民人数增加25%,则x变为4×(1+25%)=5,设至少需开N个接种台能保证2小时不再有人排队,代入公式得:24=(N-5)×2,解得N=17。选D。
(三)牛吃草的变形考查
牧场上有一片匀速生长的草地,放N头牛去吃草且每头牛每天吃的草量相同。牛吃草使草量减少,草自身生长使草量增加,(前提:牛吃草的速度小于草自身生长的速度),这种情况称之为供大于求。假设T天之后,草地的面积增加了y,每头牛每天吃1份草,这片草场的草每天的生长速度为x份。则草地增加的面积=(草每天生长的量-牛每天吃掉的量)×天数,整理可得:y=(x-N)×T。
【例2】假设一片牧场的青草一直都是“匀速”自然生长的,该牧场3月初放养有1000只羊,30天后青草的总量变为3月初的90%,此时牧场又一次性增加了300只羊。12天后青草的总量变为3月初的80%,如果要让青草在接下来4个月内(每月按30天计算)回到3月初的总量,则这4个月间该牧场至多放牧( )只羊。
A. 800 B. 750
C. 700 D. 600
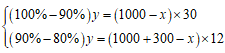
【解析】设牧场原有草量为y,草长的速度为x。列方程组:,解得x=800,y=60000。
设至多放牧N只羊,根据回到3月初的总量列方程:(100%-80%)y=(x-N)×120,即(100%-80%)×60000=(800-N)×120,解得n=700。
因此,选择C选项。
总之,无论牛吃草模型如何变化,考生只要抓住其中的速度、时间、草量三个量之间的关系,利用方程就可进行求解